本文首先回顾几种基本的非线性规划算法
然后整理求解混合整数约束非线性规划问题的文献
并且使用matlab进行算法实现
最后列举实际例子进行求解

无约束非线性规划模型

黄金分割法 golden section method

任务目标：找一维函数极小值
基本思想：步步紧逼，逐次缩小范围
- 设定搜索精度
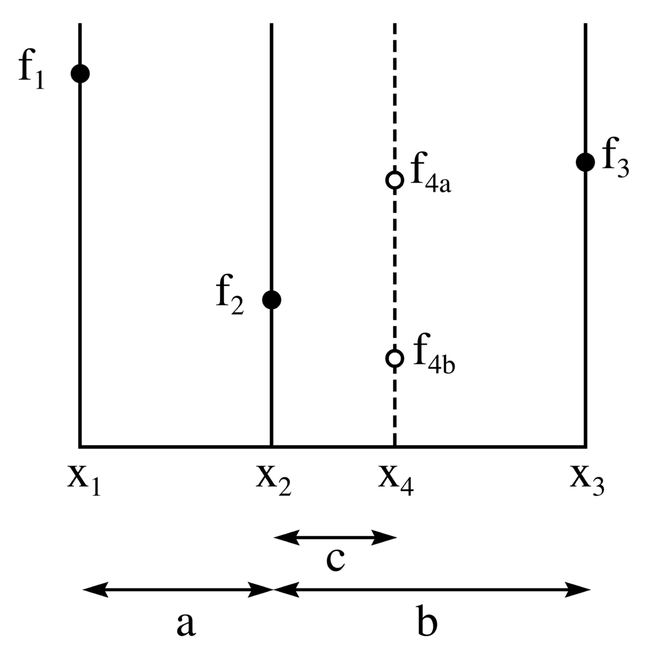
- 区间内部插入两个点，分其为三段。通过比较两个端点和插入的两个点的函数值大小，划分新的搜索区间
适用范围：一维函数，单峰函数

link - 一维搜索方法/黄金分割法（附matlab代码）

如果目标函数不是一维怎么办？多维度目标函数我们能不能转换成一维搜索？

最速下降法

任务目标：找多维函数极小值点
基本思想：多维函数一维化（负梯度方向+一维搜索方法）
- 一维化过程（确定搜索方向）：$P^{(i)}=-\nabla f(x)^{(i)}\rightarrow$ 第$i$次迭代的负梯度方向
- 一维搜索（计算搜索步长） : $f(x^{(i)}+\lambda^{(i)}P^{(i)})=\underset {\lambda>0}{\min}f(x^{(i)}-\lambda^{(i)}\nabla f(x)^{(i)})$
适用范围：目标函数容易求导，梯度方向收敛较快

但是，负梯度方向不一定是函数值下降最快方向。因为每次迭代选择的梯度方向只是起始点的梯度方向，并不能反映起始点和终点之间其他点的梯度方向。

link - 梯度下降法和最速下降法的细微差别

那么，考虑梯度的变化方向会不会加快收敛速度呢？

牛顿法（最速下降法 pro）

牛顿法就是在最速下降法的基础上添加目标函数梯度的变化的影响，也就是Hessian矩阵。
$$f(x)\approx Q(x)=f(x)^{(k)}+\nabla {(f(x^{(k)})}^T(x-x^{(k)})+\frac{1}{2}(x-x^{(k)})^T\nabla ^2f(x^{(k)})(x-x^{(k)})$$
其中$\nabla ^2f(x)$是Hessian矩阵

令 $\nabla Q(x)=0$，可以求解得到一个极小值点。
把这个极小值点作为下一次迭代点，直到小于精度时停止迭代。

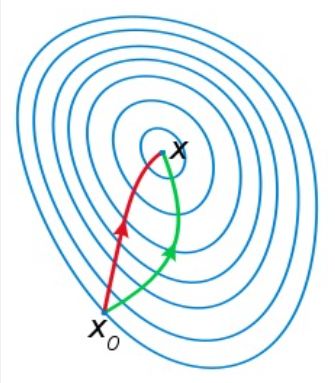
基本思想：最速下降法+Hessian矩阵
适用范围：容易求得矩阵导数，容易求得Hessian矩阵

模式搜索法

上面介绍的几种方法都需要知道一阶或者二阶导数。如果求不到导数，或者目标函数是离散的，又怎么办呢？

基本思想：多维问题一维化+每个维度左右尝试
适用范围 : 离散问题，无法求导

link - wiki:模式搜索

有约束非线性规划模型

旧问题的答案也是新问题的答案。
- Woz·G·Schwarld

有约束非线性规划模型一般数学形式：
$$ \min f(x),
s.t.\left {
\begin{aligned}
g_i(x) & \geq 0& i=0,1,…,m , \
h_i(x) & = 0& j=0,1,…,l \
\end{aligned}
\right.
$$
下面介绍的两种方法都是把有约束问题转化为无约束问题。

外点罚函数法

将约束项添加进目标函数中。当解落在可行域外时，约束项陡增，迫使解落回可行域。
内点罚函数法

仍然将约束项添加进目标函数中。但是这次所有解都在可行域中，一旦解接近范围边界，约束项就会陡增，迫使解始终在远离范围边界的可行域中迭代。

link - 罚函数法

混合整数非线性规划模型

非线性规划+整数规划

正如引言所说，旧问题的答案也是新问题的答案。
混合整数非线性规划模型可以是非线性+整数规划的叠加

整数规划	非线性规划
割平面法	罚函数法
分支定界法	可行方向法
	投影梯度法
	反应曲面法

link - 可行方向法

link - 投影梯度法

link - 复合形法

link - 反应曲面等代理模型

根据乘法原理，我们最多可以得到8种混合整数非线性规划模型，尽管他们中有些并不合理。

除此之外，各种启发式算法也可以用于求解混合整数非线性规划。

遗传算法

link - 遗传算法

模拟退火

link - 模拟退火

粒子群优化

link - 粒子群优化

代理模型算法 surrogate model

link - 代理模型

matlab算法实现介绍

代理模型

1	[x,fval,exitflag] = surrogateopt(objconstr,____)

该算法在多个维度上搜索实值目标函数的全局最小值，受多种条件约束：

目标函数 objconstr.Favl
边界 lb ub, 输入约束的下界和上界
可选不等式线性约束 A b，输入线性不等式约束
可选等式线性约束 Aeq beq，输入线性不等式约束
可选整数约束 intcon，输入为整数的变量的标号
可选非线性不等式约束obconstr.Ineq

surrogateopt函数返回一个结构体

x 返回最小值点
fval 实数解处的目标函数值
exitflag 退出标志

算法
surrogateopt重复执行这些步骤：

MinSurrogatePoints 通过在边界内随机采样点来创建一组试验点，并在试验点处评估目标函数。
通过在所有随机试验点内插径向基函数来创建目标函数的代理模型。
创建一个评价函数，为代理项赋予一些权重，对与试验点的距离赋予一些权重。通过在现有点（自上次代理重置以来找到的最佳点）周围的区域中随机采样评价函数来定位评价函数的一个小值。使用这个称为自适应点的点作为新的试验点。
在自适应点评估目标，并根据该点及其值更新代理。如果目标函数值远低于观察到的先前最佳（最低）值，则计算“成功”，否则计算“失败”。
max(nvar,5)如果在失败之前发生了 3 次成功，则向上更新样本分布的离散度，其中nvar是维数。max(nvar,5)如果失败发生在三个成功之前，则向下更新离散度。
从步骤 3 继续，直到所有试验点都在MinSampleDistance评估点范围内。此时，通过丢弃代理中的所有自适应点来重置代理，重置量表，然后返回步骤 1 以创建MinSurrogatePoints 新的随机试验点进行评估。

Solve Nonlinear Problem with Integer and Nonlinear Constraints

一个栗子

$$
\max f(x)=26(x_1-1)^2+50x_2+60x_3,\
s.t.\left{
\begin{aligned}
10 \leq 12x_1+4x_2+18x_3\
20x_1+x_2+25x_3\leq 300\
10x_1^2+4x_2+3x_3^2\leq 100\
0\leq x_i\leq 20,i=1,2,3\
x_3\in \Bbb Z\
\end{aligned}
\right.
$$

clc;clear all;close all;
%% constrain
intcon = 3;
A = [-12 -4 -18; 20 1 25];
b = [ -10;300];
lb = [0 , 0 , 0];
ub = [20 , 20 , 20];
[x,fval,exitflag] = surrogateopt(@objconstr,lb,ub,intcon,A,b);

function f = objconstr(x)
f.Fval = -( 26*( x(1) - 1 )^2 + 50*x(2) + 60*x(3) );
f.Ineq = 10 * x(1) ^ 2 + 4*x(2) + 3 * x(3)^2 -100;
end

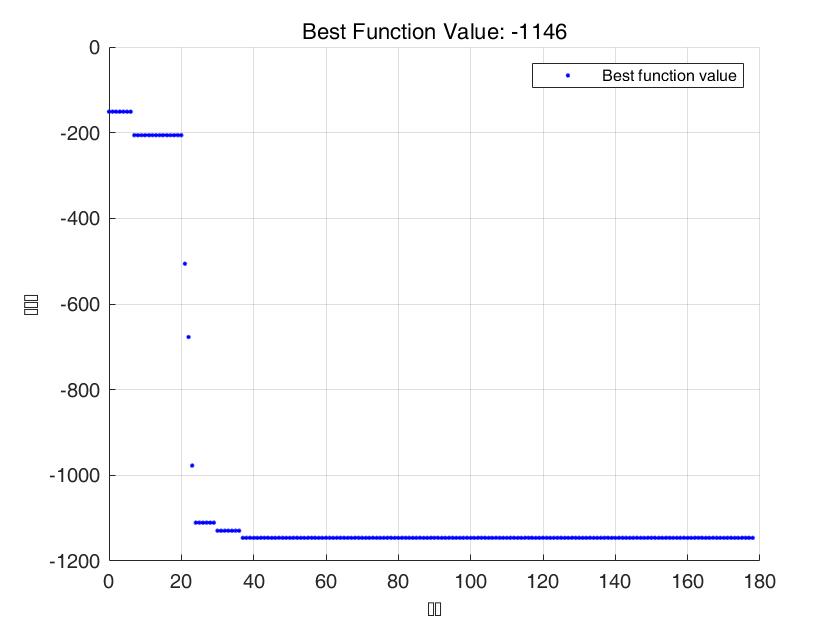
最优解为：$[ 0; 20; 2 ]$

Tianyou Zhao 的个人博客

非线性整数规划模型收纳箱